God's Handiwork -- Fibonacci Numbers

Known by the Greek letter phi, the Golden Ratio is an irrational number (i.e. one that cannot be expressed as the ratio or fraction of two whole numbers) with several curious properties. We can define it as the number that is equal to its own reciprocal plus one: phi = 1/phi + 1, with its value commonly expressed as 1.618,033,989. It's digits were calculated to ten million places in 1996, and they never repeat. It is related to Fibonacci numbers in that if you divide two consecutive numbers in the Fibonacci sequence, the answer is always an approximation of phi.

Also known as the Divine Proportion, the Golden Mean, or the Golden Section, this ratio is found with surprising frequency in natural structures as well as man-made art and architecture, where the ratio of length to width of approximately 1:1.618 is seen as visually pleasing. It is the point dividing a distance into two segments where the proportion of the smaller segment to the larger segment is the same as the larger to the whole.

Leaves On A Stem

If we look down on a plant, the leaves are often arranged so that leaves above do not hide leaves below. This means that each gets a good share of the sunlight and catches the most rain to channel down to the roots as it runs down the leaf to the stem.

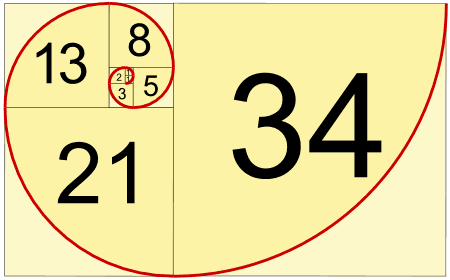
The Fibonacci numbers occur when counting both the number of times we go around the stem, going from leaf to leaf, as well as counting the leaves we meet until we encounter a leaf directly above the starting one. If we count in the other direction, we get a different number of turns for the same number of leaves. One estimate is that 90 percent of all plants exhibit Fibonacci numbers in their leaf patterns.
Some common trees with their Fibonacci leaf arrangement numbers are:

1/2 elm, linden, lime, grasses
1/3 beech, hazel, grasses, blackberry
2/5 oak, cherry, apple, holly, plum, common groundsel
3/8 poplar, rose, pear, willow
5/13 pussy willow, almond

The numerator is # of turns and denominator is # of leaves til we arrive at a leaf directly under the starting leaf. Each leaf is this fraction of a turn after the last leaf. Or, there are so many turns (numerator) for every so many leaves (denominator).

Cactus's spines often show the same spirals as we see on pine cones, petals and leaf arrangements, but they are much more clearly visible.

Plants illustrate the Fibonacci series in the numbers and arrangements of petals, leaves, sections and seeds. Plants that are formed in spirals, such as artichokes, pinecones, pineapples, daisies and sunflowers, illustrate Fibonacci numbers.  For instance, the pineapple rind has eight gently-sloping spirals (left), thirteen steeper-sloping spirals (center) and twenty-one almost vertical spirals (right). A Fibonacci series. Many plants produce new branches in quantities that are based on Fibonacci numbers.

Calla Lilies have one petal. Euphorbia have two petals. Lilies have three. Buttercups, Roses, Pinks and Geraniums have five, Delphiniums and Bloodroot have 8 petals, Marigolds and Ragworts have 13, Asters and Black-eyed Susans 21, Pyrethrum have 34, and most Daisies have 34, 55, or 89. You don't find any other numbers very often. 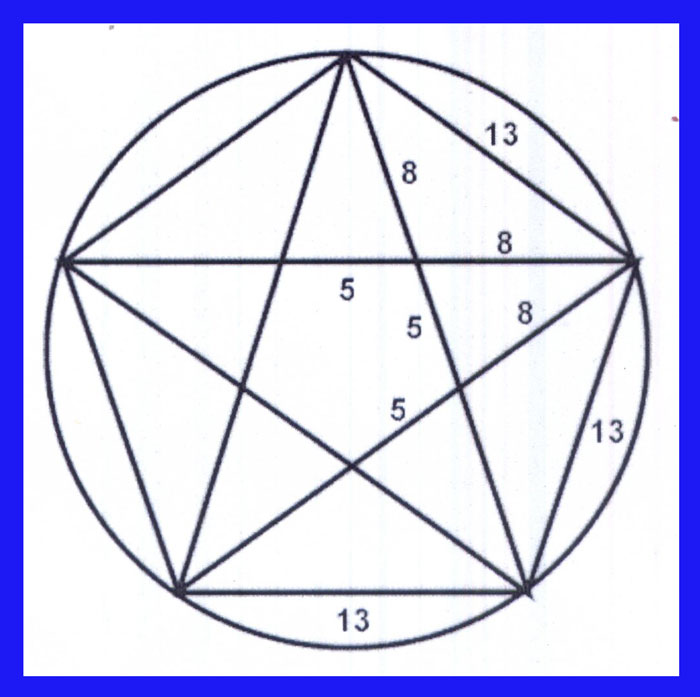(The main exceptions are when those same numbers appear doubled, or when the so-called anomalous series appears: 3, 4, 7, 11, 18 and so on.). The five-pointed star is unusually common in nature. Not only in flowers, but also in the starfish, sand dollar, apple, etcetera. Why? Because Phi is the ratio of the side of a pentagon to its diagonal (see picture). “To see a world in a grain of sand and heaven in a wild flower Hold infinity in the palms of your hand and eternity in an hour.” -William Blake

The Sunflower, Pinecone, Daisy and Nautilus Shell

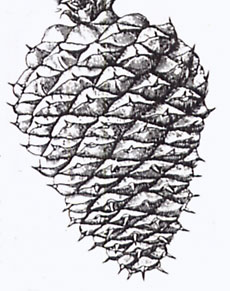
Furthermore, the SUNFLOWER has 21 spirals on its head in one direction and 34 going in the other -- consecutive Fibonacci numbers. Or 34 and 55, or 55 and 89, or 89 and 144. The precise numbers depend on the species of SUNFLOWER.The same is true with DAISIES. The outside of a PINECONE has spirals that run clockwise and counterclockwise, and the ratio of the number of spirals is sequential Fibonacci values. In the elegant curves of a NAUTILUS shell, each complete new revolution will be a ratio of 1:1.618, when compared to the distance from the center of the previous spiral. 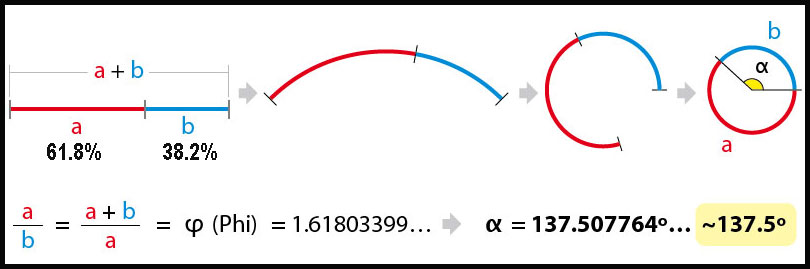If the divergence angle of a SUNFLOWER varies from 137.5 degrees (seen in the pattern below) to either 137.4 or 137.6 degrees, much of the beauty of the spiral is lost as well as its most compact arrangement. The SUNFLOWER therefore is in a precise state of perfection. ROMANESQUE BROCCOLI/CAULIFLOWER is Fibonacci spiral upon spiral. The same can be said of any other plant or animal containing this Fibonacci sequence. Everything in nature is already in a state of perfection -- contrary to the theory of Evolution. Where are the transitional stages? Where are the vestigial organs? Where are the imperfect spirals? 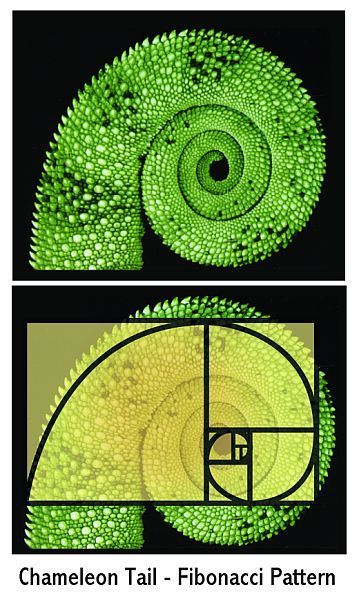Who told a DAISY to have the same Fibonacci sequence as a NAUTILUS, or a PINECONE, or a SUNFLOWER, or a RAM'S HORN or even the appearance of a BREAKING WAVE? Who told the FIDDLEHEAD to have the same Fibonacci sequence as FERNS, CACTUS SPINES, the TAILS of a LIZARD or SEAHORSE, a LILY, a WEB, a TUSK, a CLAW, or BEAK or FINGERPRINT. None of them have a brain. None of them are in any way related to the other. Design demands a Designer. 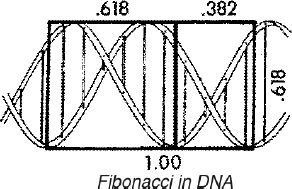Beauty demands a Master Artist. They were created flawlessly. These animals and plants are unaware of mathematics and a breaking wave can't even think. Even the structure of the DNA spiral is 21 angstroms wide by 34 angstroms long. As William Blake stated, "To see the world in a grain of sand, and a heaven in a wild flower; Hold infinity in the palm of your hand, and eternity in an hour."

The Human Head

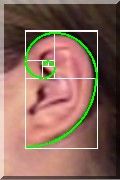
Human beauty is based on the Divine Proportion. Many experiments have been carried out to prove that the proportions of the top models' faces conform more closely to the Golden Ratio than the rest of the population. The human face is based entirely on Phi .The head forms a golden rectangle with the eyes at its midpoint.  The mouth and nose are each placed at golden sections of the distance between the eyes and the bottom of the chin.  The ear reflects the shape of a Fibonacci spiral. Even the dimensions of our teeth are based on phi. The front two incisor teeth form a golden rectangle, with a phi ratio in the heighth to the width. The ratio of the width of the first tooth to the second tooth from the center is also phi. The ratio of the width of the smile to the third tooth from the center is phi as well.

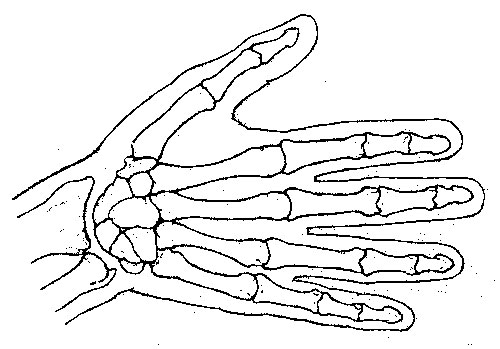
The Human Finger Joints and Hand

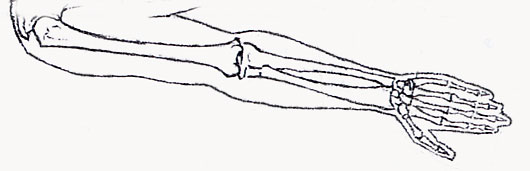
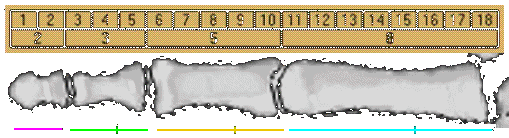
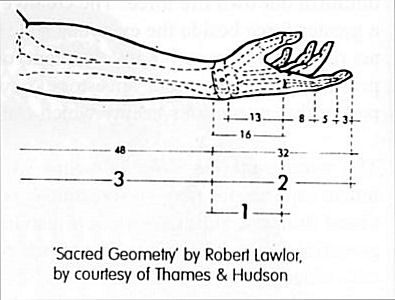
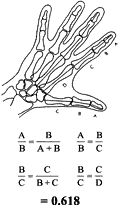
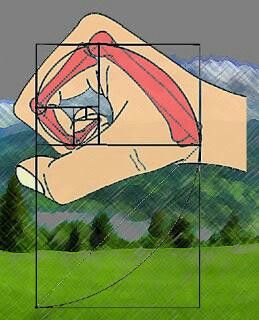
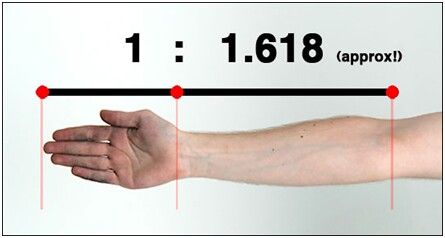
Each segment of each finger, from the tip to the base of the wrist, is larger than the preceding one by about the Fibonacci ratio of 1.618. In other words, the smallest segment is 2, the next 3, the next 5, and the back of your hand is 8. By this scale, your fingernail is 1 unit in length. You also have 2 hands, each with 5 digits, and your 8 fingers are each comprised of 3 sections.  All Fibonacci numbers! Your hand creates a golden section in relation to your forearm, as the ratio of your forearm to your hand is also 1.618, the Divine Proportion. Furthermore, your hand and forearm together are a golden section in relation to the entire length of your arm.

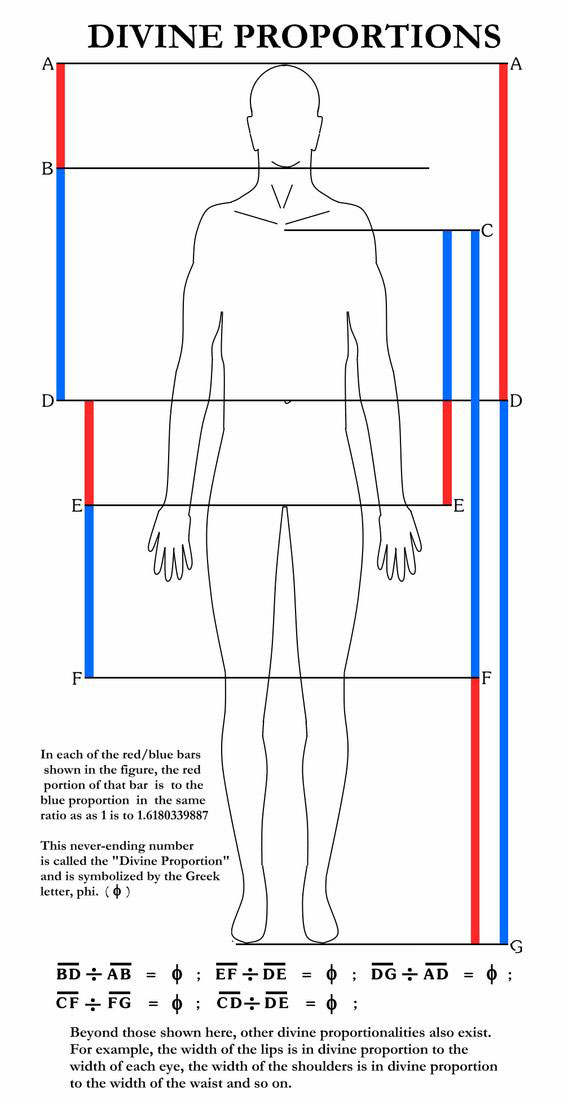
The Human Body

The ventricles of the human heart reset themselves at the Golden Ratio point of the heart's rhythmic cycle.

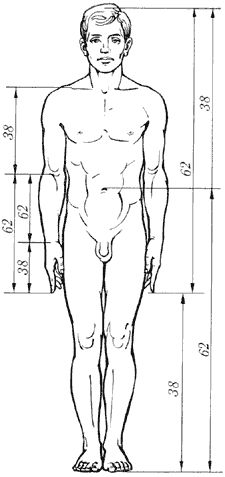
Leonardo Da Vinci found that the total height of the human body, from toes to top of head, and the height from the toes to the navel depression are in Golden Ratio. Also the height from toes to navel and from the navel to the top of the head are in Golden Ratio. This has been confirmed by measuring 207 students at the Pascal Gymnasium in Munster Germany, where the perfect value of 1.618 was obtained for the first ratio average and 1.619 was obtained for the second. This value held for both girls and boys of similar ages ("Golden Mean of the Human Body" by T. Antony Davis and Rudolf Altevogt).

But there is more. From the top of the head to the bottom of the feet is the body's total height A. From the top of the head to the bottom of the fingertips is a golden section B of the total height A. From the top of the head to the navel and elbows is a golden section C of the golden section B. From the top of the head to the pectorals and armpits, the width of the shoulders, the length of the forearm and shinbone is a golden section D of the golden section C. From the top of the head to the base of the skull and the width of the abdomen is a golden section E of the golden section D. The width of the head and half the width of the chest and the hips is the golden section F of the golden section E.

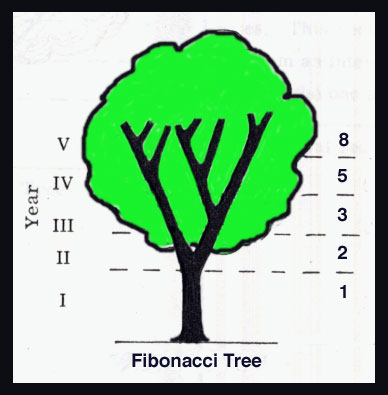
The human body is also based on the number 5: The torso has 5 appendages, in the arms, legs and head. In turn, each of these has five appendages, in the fingers and toes and 5 openings on the face. and 5 senses in sight, sound, touch, taste and smell. The golden section is also based on 5, as the number phi, or 1.6180339 is computed from the square root of 5 multiplied by .5 plus .5 = Phi. Bronchi in lungs are designed like a Fibonacci tree.

Relative Planetary Distances

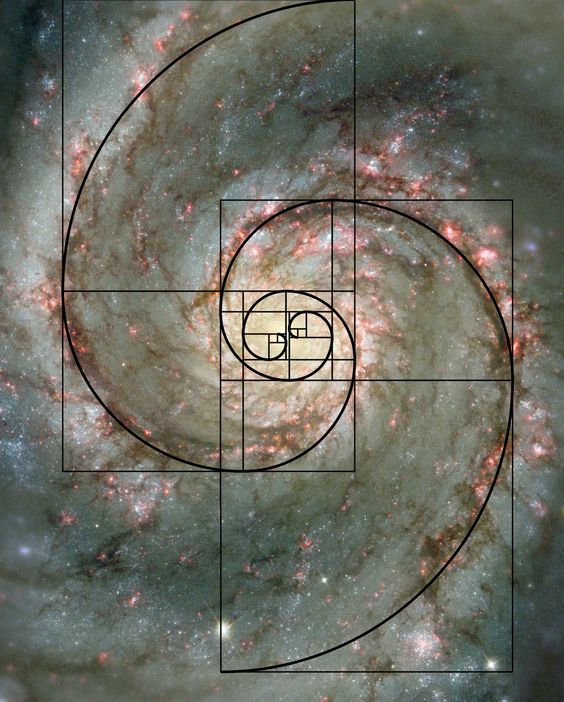
Galaxies conform to the same Fibonacci spiral as the Nautilus sea shell. The Aurora Borealis conforms to Fibonacci numbers. The relative planetary distances average to Phi. The average of the mean orbital distances of each successive planet in relation to the one before it approximates phi: The mean distance is in million kilometers per NASA. If Mercury is 1, these are the relative mean distances Mercury 57.91 (1.00000) Venus 108.21 (1.86859) Earth 149.60 (1.38250) Mars 227.92 (1.52353) Ceres (the largest asteroid) 413.79 (1.81552) Jupiter 778.57 (1.88154) Saturn 1,433.53 (1.84123) Uranus 2,872.46 (2.00377) Neptune 4,495.06 (1.56488) and Pluto 5,869.66 (1.30580) The total is 16.18736 and so if we divide by 10, we get the average which is1.61874. Phi is1.61803.

The Fibonacci Series also predicts accurately the distances of the moons of Jupiter, Saturn and Uranus from each one's respective parent planet. Individual offsets can be attributed to planetary densities. Jupiter has 12 moons. Saturn has 9 moons and Uranus has 5 moons. For actual plotted graphs of these amazing results refer to the Fibonacci Quarterly October 1970, vol. 8, Number 4.

The Golden ratio (1.618) is related to the sidereal and synodic years of all planets until Uranus to a statistical significance of over 99%.
A planet's Sidereal year is the time it takes for that planet to revolve around the sun so as to line up with the background stars. It is the only type of planetary year we are able to measure at this point; An interplanetary synodic is the time it takes for one planet to "lap" another in their revolutions around the earth.

Mercury's sidereal year is 88 days. The Mercury-Venus synodic is 144.5255474 days. 88x1.61803 = 142.387, which is within 2 percent of the Mercury-Venus synodic.
The Mercury-Venus synodic is 144.5255474 days. Venus's sidereal year is 225 days. 144.5255x1.61803 = 233.84, which is within 4% of Venus's sidereal year
Venus's sidereal year is 225 days. Earth's sidereal orbit is 365.24 days. 225x1.61803 = 364.05, which is within .3% of Earth's sidereal orbit;
Earth's sidereal orbit is 365.24 days. Mars's sidereal orbit is 686.9601. 365.24x1.61803=590.969, which is within 13% of Mars's sideral orbit.
Mars's sidereal orbit is 686.9601 days. The Mars-Ceres synodic is 1161.588 days. 365.24x1.618=1111.4, within 4% of the Mars-Ceres synodic.
The Mars-Ceres synodic is 1161.588 days. The orbit of Ceres is 1681.24 days. 1161.588x1.618=1879.4, within 10% of the orbit of Ceres.
Ceres's orbit is 1681.24 days. Jupiter's orbit is 2746.223 days. 1681.24 daysx1.618 = 2720, within 1% of the orbit of Jupiter.
Jupiter's orbit is 2746.223 days. The Jupiter-Saturn synodic is 3687.59 days. 2746.223x1.618= 4443, within 17% of the Jupiter-Saturn synodic.
The Jupiter-Saturn synodic is 7261.85 days. The orbit of Saturn is 10757.73 days. 7261.85*1.6180339887=11,748, within 8% of the orbit of Saturn.
The orbit of Saturn is 10,757.73 days. The Saturn-Uranus synodic is 16,558.56 days. 10,757.73x1.61803=17,406.3, within 5% of the Saturn-Uranus synodic.
The Saturn-Uranus synodic is 16,558.56 days. The orbit of Uranus is 30,708.16 days. 16,58.56x1.61803 = 26792, within 12% of the orbit of Uranus.
The orbit of Uranus synodic is 30,708.16 days. The Uranus-Pluto synodic is 46,449.19781. 30,708.16x1.61803 = 49686.46524, within 7% of the Uranus-Pluto synodic.
The Uranus-Pluto synodic is 46449.19781 days. The orbit of Pluto is 90,613.31 days. 90,613.31x1.61803 = 75156.19554, within 17% of the orbit of Uranus.

The deviations are small in comparison to the similarities. In fact, the planets deviate from the series less than 1/1000 of one percent. Yet why are there deviations at all?
Because of orbital variation over time: for instance equinox precession: If the sun is moving as argued by the binar theory, then the tropical year, rather than the sideral year is the true year. The tropical year, while close to the sidereal year, differs somewhat. Also imprecision in measurements.

Why doesn't Neptune fit into the pattern? Because it is a half-way marker between Uranus and Pluto.

The universe is not a random accident. It is a finely tuned and engineered creation of living and non-living matter that all conforms to 1.618 or Fibonacci numbers.
No naturalistic explanation has been proposed to explain the yearly cycles of planets conforming to the golden ratio. Creationists point out that in order for this to take place, all of the planets had to be a particular mass in order to move at a particular period at a particular distance. If any of them had been smaller than they are, the pattern would not exist. If any of them had been bigger than they are, the pattern would not exist. Thus there is evidence that the size of the planets was deliberately chosen to make the planets move in a particular and aesthetic harmony. To creationists, it is no surprise to find harmony engineered into the planets by the Great Engineer.

The Greatest Human Achievements Include the Golden Ratio

The dimensions of the King's Chamber of the Great Pyramid in Giza, Egypt are based upon the Golden Ratio. The Great Pyramid's vertical height and the width of any of its sides are in Golden Sections. The architect, Le Corbusier designed his Modulor system around the use of the ratio; the painter Mondrian based most of his work on the Golden Ratio; Leonardo Da Vinci included it in many of his paintings and Claude Debussy used its properties in his music. So did Bela Bartok. 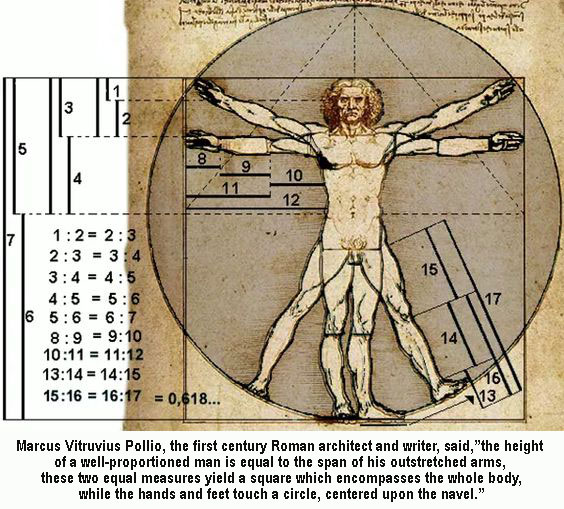The Golden Ratio also is found in widescreen televisions, postcards, credit cards, and photographs which all commonly conform to its proportions. Like the brilliant Pythagoras before him, Leonardo had made an in-depth study of the human figure, showing how all of its major parts were related to the Golden Ratio. The Mona Lisa's face fits inside a perfect Golden Rectangle. The Golden Rectangle is found in his painting called The Last Supper also. Many other Renaissance artists did the same. After Leonardo, artists such as Raphael and Michelangelo made great use of the Golden Ratio to construct their works. Michelangelo's beautiful sculpture of David conforms to the Golden Ratio, from the location of the navel with respect to the height and placement of the joints in the fingers. The builders of the medieval and Gothic churches and cathedrals of Europe also made these structures conform to the Golden Ratio. The Golden Rectangle is one whose sides are in the proportion of the Golden Ratio. This means the longer side is 1.618 times longer than the shorter side. The front of the Parthenon in Athens, Greece can be framed within a Golden Rectangle. Da Vinci's drawing of the Vitruvian Man has the outlines of a rectangle based on the head, one on the torso, and another over the legs.

The Golden Ratio In The Bible

The Ark of the Covenant is a Golden Rectangle. In Exodus 25:10, God commands Moses to build the Ark of the Covenant, in which to hold His Covenant with the Israelites, the Ten Commandments, saying,"Have them make a chest of acacia wood -- two and a half cubits long, a cubit and a half wide, and a cubit and a half high." The ratio of 2.5 to 1.5 is 1.666..., which is as close to phi (1.618 ...) as you can come with such simple numbers and is certainly not visibly different to the eye.  The Ark of the Covenant is thus constructed using the Golden Section, or Divine Proportion.  This ratio is also the same as 5 to 3, numbers from the Fibonacci series.

Noah's Ark uses a Golden Rectangle. In Genesis 6:15, God commands Noah to build an ark saying,"And this is the fashion which thou shalt make it of: The length of the ark shall be three hundred cubits, the breadth of it fifty cubits, and the height of it thirty cubits."Thus the end of the ark, at 50 by 30 cubits, is also in the ratio of 5 to 3, or 1.666..., again a close approximation of phi not visibly different to the naked eye.  Noah's ark was built in the same proportion as ten arks of the covenant placed side by side.

Exodus 27:1-2 mentions the dimensions of the altar -- constructed according to phi: "Build an altar of acacia wood, three cubits high; it is to be square, five cubits long and five cubits wide."

Furthermore, the location of Jerusalem is 31 degrees 45 minutes north of the equator. God said Jerusalem is "the city which I have chosen to put my name there" (1 Kings 11:36). Why did God select this location? First build a rectangular building in Jerusalem with sides that exhibit the golden rectangle ratio. The longer two sides (1.618) must run from east to west. The shorter two sides (1) must run from north to south. Then at each of the four corners place a flag pole. Make the roof flat. Remember that the sun rises in the east and sets in the west. Now if you draw one diagonal line from the northwest to the southeast corner, and another diagonal line from the northeast to southwest corner, you will create angles of 31 degrees 45 minutes with respect to the straight line joining the two southern corners of the building. At the summer solstice, the sun is over the Tropic of Cancer, 23.5 degrees north of the equator. At this point the shadows will point most easterly and westerly. At the winter solstice, the sun is over the Tropic of Capricorn, 23.5 degrees south of the equator. At this point the shadows will point most northerly. On the spring (March 21) and fall (Sept. 23) equinoxes, when the sun is directly over the equator, the shadows created by sunrise and sunset will fall exactly on these diagonal lines. This method can be used at any latitude with rectangles of different proportions. But a rectangle with the proportions of "the golden section " will only give this result at the exact latitude of Jerusalem. It is important to know when the equinoxes occur each year in order to celebrate God's festivals. We are to take the first new moon on or after the spring equinox as New Year's Day. No complex postponement rules or calculated calendar is necessary. Babylon is about one degree further north than Jerusalem. The pyramids of Gizeh are further south and Mecca still further south.

Fibonacci Numbers In The Musical Scale

The musical scales are based on Fibonacci numbers. 1,1,2,3,5,8,13. The piano keyboard scale of C to C has 8 white keys in an "octave" and 5 black keys, making 13 keys total. The 5 black keys are divided into groups: of 2 keys and 3 keys. A scale is comprised of 8 notes, of which the 5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale. Although there are only 12 notes in the scale, if you don't have a root and octave, a start and an end, you have no means of calculating the gradations in between, so this 13th note as the octave is essential to computing the frequencies of the other notes.  The word "octave" comes from the Latin word for 8, referring to the eight whole tones of the complete musical scale, which in the key of C are C-D-E-F-G-A-B-C.

In a scale, the dominant note is the 5th note of the major scale, which is also the 8th note of all 13 notes that comprise the octave.  This provides another instance of Fibonacci numbers in key musical relationships.  Interestingly, 8/13 is .61538, which approximates phi.  What's more, the typical three chord song in the key of A is made up of A, its Fibonacci & phi partner E, and D, to which A bears the same relationship as E does to A. This is analogous to the "A is to B as B is to C" basis for the golden section, or in this case "D is to A as A is to E."

Musical frequencies are based on Fibonacci ratios. Notes in the scale of western music have a foundation in the Fibonacci series, as the frequencies of musical notes have relationships based on Fibonacci numbers: A440 Hertz is an arbitrary standard.  The American Federation of Musicians accepted the A440 as standard pitch in 1917.  It was then accepted by the U.S. government as its standard in 1920 and it was not until 1939 that this pitch was accepted internationally.  Before recent times a variety of tunings were used.  It has been suggested by James Furia and others that A432 be the standard.  A432 was often used by classical composers and results in a tuning of the whole number frequencies that are connected to numbers used in the construction of a variety of ancient works and sacred sites, such as the Great Pyramid of Egypt.  The controversy over tuning still rages, with proponents of A432 or C256 as being more natural tunings than the current standard.

Most music worldwide has been tuned to 440 hertz since the International Standards Organization (ISO) endorsed it in 1953. The recent rediscoveries of the vibratory / oscillatory nature of the universe indicate that this contemporary international concert pitch standard may generate an unhealthy effect or anti-social behavior in the consciousness of human beings. A=432 Hz, known as Verdi’s ‘A’ is an alternative tuning that is mathematically consistent with the universe. Music based on 432 Hz transmits beneficial healing energy, because it is a pure tone of math fundamental to nature. There is a theory that the change from 432 Hz to 440 Hz was dictated by Nazi propaganda minister, Joseph Goebbels. He used it to make people think and feel a certain manner, and to make them a prisoner of a certain consciousness. Then around 1940 the United States introduced 440 Hz worldwide, and finally in 1953 it became the ISO 16-standard. What is 440 Hz? 440 Hz is the unnatural standard tuning frequency, removed from the symmetry of sacred vibrations and overtones that has declared war on the subconscious mind of Western Man. In a paper entitled ‘Musical Cult Control’, Dr. Leonard Horowitz writes: “The music industry features this imposed frequency that is ‘herding’ populations into greater aggression, psycho social agitation, and emotional distress predisposing people to physical illness.” You just have to go out in the street and take a look around. What do you see? School kids, young adults on their way to work, a woman pushing her baby in a pram, a man walking his dog – and what do they all have in common? iPods or MP3 Players! Ingenious, isn't it?

“If you want to find the secrets of the universe, think in terms of energy, frequency and vibration.” -Nikola Tesla
The powers that be are successfully lowering the vibrations of not only the young generation but the rest of us as well. These destructive frequencies entrain the thoughts towards disruption, disharmony and disunity. Additionally, they also stimulate the controlling organ of the body - the brain - into disharmonious resonance, which ultimately creates disease and war. Hear the difference between 432 Hz and 440 Hz. “This unnatural standard tuning frequency (440 Hz), removed from the symmetry of sacred vibrations and overtones, has declared war on the subconscious mind of Western Man.” -L. C. Vincent

The Hidden Power of Universal Frequency and Vibration Frequency and vibration hold a critically important yet hidden power to affect our lives, our health, our society and our world. The science of Cymatics (meaning the study of visible sound and vibration) proves that frequency and vibration are the master keys and organizational foundation for the creation of all matter and life on this planet. When sound waves move through a physical medium (sand, air, water, etc.) the frequency of the waves has a direct effect upon the structures which are created by the sound waves as they pass through that particular medium.

“If one should desire to know whether a kingdom is well governed, if its morals are good or bad, the quality of its music will furnish the answer.” -Confucius
Music has a hidden power to affect our minds, our bodies, our thoughts, and our society. When that music is based upon a tuning standard purposely removed from the natural harmonics found in nature, the end result may be the psychic poisoning of the mass mind of humanity. As Kymatica Documentary (2009) says: The rediscovered knowledge of the science of sound shows that sound is something more than mere vibratory signals, not only does sound interact with life but it sustains and develops it. It acts as a conduit of conscious intent between people, societies and entire civilizations.

Article sources:
Attuned Vibrations (attunedvibrations.com)
The Importance of 432 Hz Music (omega432.com)
The Rockefeller Foundation’s War on Consciousness through Imposition Of 440 Hz Standard Tuning (medicalveritas.org)
Water Sound Images (watersoundimages.com)
The Missing Secrets Of Nikola Tesla (knowledgeoftoday.org)
Source: whydontyoutrythis.com

Musical compositions often reflect Fibonacci numbers and phi Fibonacci and phi relationships are often found in the timing of musical compositions.  As an example, the climax of songs is often found at roughly the phi point (61.8%) of the song, as opposed to the middle or end of the song.  In a 32 bar song, this would occur in the 20th bar.